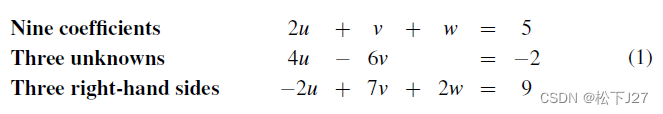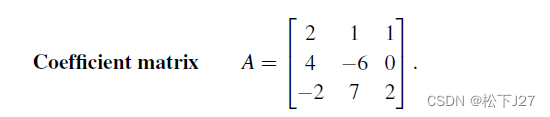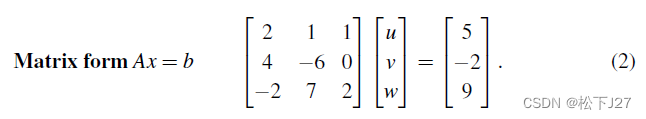线性代数

您所在的位置：网站首页 › 线性代数向量 › 线性代数

线性代数

2024-07-16 00:19| 来源: 网络整理| 查看: 265

矩阵与向量相乘

part I 矩阵与向量的乘法：

矩阵x列向量（注：可以把列向量看成是nx1的矩阵）

现有如下方程组：

9个系数，3个未知数，等式右边有3个数

上述方程组可用矩阵的方式改写成，一个系数矩阵A与一个未知数向量x的乘积，乘积的结果等于右端向量b：

现在我们分别用两种方法，逐行点乘和各列的线性组合来计算系数矩阵A和未知数向量x的乘法。

第一种方法，逐行点乘：

用A矩阵中的每一行row去乘以x，如下

用这种计算方法得到的结果，正好是原始方程组中的第一个方程的左边。依此类推，也就是用A矩阵中的第二，第三行，逐一与向量x相乘，就能得到整个原始方程组的左边。

$\begin{bmatrix} 2 &1 &1 \\ 4&-6 &0 \\ -2&7 &2 \end{bmatrix} \begin{bmatrix} u \\v \\w \end{bmatrix} = \begin{bmatrix} 2u+v+w\\ 4u-6v\\ -2u+7v+2w \end{bmatrix}$

补充图示：

Tips:(点乘/内积)

一个1xn的行向量乘以一个nx1的列向量是一个非常基本的操作，他会得到一个数1x1。这个算法又叫矩阵的内积（Inner product）或点乘。例如，用A中的第一行[2 1 1]乘以另外一个列向量[1 1 2]，得到的就是一个数[5]。

第二种方法，各列的线性组合：

把b看成是A中各个列向量(column)与未知数向量x的线性组合，其中，u,v,w分别代表了矩阵A中第1，2，3列所对应的权重。

$u\begin{bmatrix} 2 \\ 4 \\-2 \end{bmatrix}+v\begin{bmatrix} 1 \\ -6 \\7 \end{bmatrix}+w\begin{bmatrix} 1 \\ 0 \\2 \end{bmatrix}=\begin{bmatrix} 2u \\ 4u \\-2u \end{bmatrix}+\begin{bmatrix} v \\ -6v \\7v \end{bmatrix}+\begin{bmatrix} w \\ 0 \\2w \end{bmatrix}\\ = \begin{bmatrix} 2u+v+w\\ 4u-6v\\ -2u+7v+2w \end{bmatrix}$

这种计算方法与思考方式应当成为首选，更是学习线性代数该有的视角(强烈推荐)。因为他是在用线性组合的方式来看问题。（在后面的学习中，我们会用空间Space这种更高的视角来看Ax=b。）就好像我在另外一篇自己的学习总结中写的那样，学习线性代数的重点，不应该是只学习如果求解Ax=b，而是去学习如果表达Ax=b。

补充图示：

行向量x矩阵（注：可以把行向量看成是1xn的矩阵）

同理，对于另一种向量，行向量而言，也有相似的两种算法。所不同的是，列向量的乘法矩阵在向量之前，而行向量的乘法，矩阵在向量之后。

1，逐列点乘

2，各行的线性组合

矩阵与矩阵相乘

part II 矩阵与矩阵的乘法：

有了前面的基础知识，我们就应该摈弃早年学习线性代数时早已形成的那种，用矩阵A中的每一行乘x的方式去计算Ax中的每一个元素。而是应该尝试着去考虑上文中提到的线性组合视角。矩阵与矩阵相乘分为矩阵的左(前)乘与矩阵的右(后)乘。矩阵的右(后)乘即为对矩阵A的列操作，而矩阵的左(前)乘即为对矩阵A的行操作。

矩阵的右(后)乘：矩阵B右乘矩阵A，AB

假设矩阵A的维度是axb，矩阵B的维度是bxc

矩阵B后(右)乘矩阵A。首先，把矩阵B看成一个个列向量 $col_{1}$ , $col_{2}$ ...... $col_{c}$ ，共计c列，其中每个列向量都有b个元素。其次，把这些列向量中的元素看成对A中各列线性组合的权重，即， $col_{1}=W_{1},col_{2}=W_{2},...,col_{c}=W_{c}$ ，每个W都有b个子权重。

B中每个col与矩阵A各列的计算结果都是一个ax1的列向量，作为新矩阵AB的一列。因为矩阵B有c个col，因此要计算c次，得到c个ax1的列向量，矩阵AB最终是一个axc的矩阵。

（牢记口诀：后乘矩阵，列操作。）

矩阵的左(前)乘：矩阵B左乘矩阵A，BA

假设矩阵A的维度是nxj，矩阵B的维度是ixn

矩阵B左乘矩阵A。首先，把矩阵B看成一个个行向量 $row_{1}$ , $row_{2}$ ,... $row_{i}$ ，共计i行，其中每个行向量都有n个元素。其次，把这些行向量中的元素看做对A中各行线性组合的权重，即， $row_{1}=W_{1},row_{2}=W_{2},...,row_{i}=W_{i}$ ，每个W都有c个子权重。